Paper Review - 'ANOMALY TRANSFORMER: TIME SERIES ANOMALYDETECTION WITH ASSOCIATION DISCREPANCY'

해당 논문은 ICLR( International Conference on Learning Representations )에 2022년 출판된 학술 논문입니다.

저자: Jiehui Xu∗ , Haixu Wu∗ , Jianmin Wang, Mingsheng Long

1. INTRODUCTION

• 이상 징후 탐지의 과제: 실제 시스템은 다중 센서에 의해 모니터링되는 지속적인 데이터를 생성한다. 이러한 데이터 스트림에서 이상 징후를 탐지하는 것은 보안 침해와 재정적 손실을 방지하는 데 매우 중요하다. 그러나 이상 징후는 드물고 방대한 양의 정상 데이터에 의해 가려지는 경우가 많아 식별하기 어렵고 레이블을 지정하는 데 비용이 많이 든다.
• 고전적 방법의 한계: LOF 및 1-클래스 SVM과 같은 전통적인 이상 탐지 방법은 시간 정보를 고려하지 않기 때문에 실제 시나리오에서 효과가 제한된다.
• 트랜스포머 사용의 장점: 본 논문에서는 시계열 이상 탐지를 위해 자연어 처리 및 컴퓨터 비전과 같은 분야에서 높은 성공을 거둔 모델의 일종인 트랜스포머를 사용할 것을 제안한다. 트랜스포머는 글로벌 표현과 장거리 종속성을 모델링할 수 있어 시계열 데이터에 대한 이해가 풍부하기 때문에 이 작업에 특히 적합하다.
• 이상 징후 트랜스포머: 이 새로운 모델은 두 갈래 구조를 사용하여 로컬(사전 연관) 및 글로벌(직렬 연관) 시간 관계를 모두 포착하는 이상 징후 주의 메커니즘을 도입한다. 이상 징후는 인근 시점과 더 강한 연관성을 보이는 경향이 있으며, 이는 모델이 정상 데이터와 구별하기 위해 활용하는 특징이다.
• Association Discrepancy: Association Discrepancy은 로컬 및 글로벌 연관성의 차이를 기반으로 이상 징후를 식별하는 협회 불일치 개념이다. 이 불일치는 이상 징후를 보다 효과적으로 정량화하고 감지하는 데 사용된다.
• 결과 및 기여: 변칙 트랜스포머는 여러 벤치마크와 실제 애플리케이션에서 최첨단 성능을 보여준다. 고유한 주의 메커니즘과 모델의 정상 지점과 비정상 지점을 구별하는 능력을 향상시키는 미니맥스 접근법의 전략적 사용을 통해 이를 달성한다.

전반적으로, ANOMALY TRANSFORMER는 트랜스포머 아키텍처의 강점을 활용하고 시계열 데이터의 뉘앙스에 맞게 조정함으로써 감독되지 않은 시계열 이상 탐지에 대한 유망한 새로운 접근 방식을 제공한다.

2. Method

이 절에서는 시계열 데이터의 이상 징후를 탐지하는 방법에 대해 설명한다.

• 시스템 모니터링: 이 방법은 동일한 시간 간격으로 기록된 여러 측정값(\(d\))으로 시스템을 모니터링하는 것입니다. 시계열 데이터는 점 \(x_1, x_2, ..., x_N\)으로 구성된 \(X\)로 표시되며, 여기서 \(\mathbb{R}^d\)의 각 \(x_t\)는 시간 \(t\)에서의 관측값이다.
• Unsupervised Anomaly Detection: 목표는 이를 나타내는 레이블 없이 각 관측값 \(x_t\)이 정상인지 비정상인지 여부를 결정하는 것이다. 이는 무엇이 정상 또는 비정상 행동을 구성하는지에 대한 사전 레이블이 없이 수행되어야 하기 때문에 어렵다.
• Anomaly Transformer: 이 문제를 해결하기 위해 이 방법은 " Anomaly Transformer "를 도입한다. 이 도구는 정상과 비정상 관측치를 구별하는 데 도움이 될 수 있는 데이터 내의 정보적 연관성을 학습하는 데 중점을 둔다.
• Association Discrepancy: 도입된 핵심 개념은 "Association Discrepancy"로, 고유한 연관성을 기반으로 정상 데이터와 비정상 데이터를 구별하는 능력이다. 이는 두 가지 유형의 연관성을 학습함으로써 달성된다.
  • Prior-association: 과거 데이터를 기반으로 예상되거나 일반적인 패턴을 캡처한다.
  • 직렬 연관: 현재 데이터에서 실제 관찰된 패턴을 캡처한다.
• Minimax Optimization: 이러한 연관성과 함께 연관성 불일치의 구별 가능성을 높이기 위해 Minimax Optimization을 사용한다. 이 전략은 이상 탐지의 견고성을 보장하기 위해 최악의 경우(최대 손실) 시나리오를 최적화하는 것을 포함한다.
• Association-Based Criterion: 이 기준은 관측치가 예상되는 것(이전)과 관측된 것(계열)을 얼마나 벗어났는지에 기초한다.

3.1 ANOMALY TRANSFORMER

 

계층 아키텍처: Anomaly Transformer는 시계열 데이터에서 복잡한 다단계 기능을 학습하는 모델의 기능을 향상시키기 위해 설계된 Anomaly-Attention 메커니즘과 교대 feed-forward계층을 통합하여 표준 트랜스포머 아키텍처를 수정한다.

•  \(Z^l\): 정규화 후 레이어 \(l\)에서  Anomaly-Attention 메커니즘의 출력을 나타낸다. 이전 레이어의 출력(\(Y^{l-1}\)에 대한 Anomaly-Attention의 출력을 \(Y^{l-1}\) 자체에 더한 다음 레이어 정규화를 적용하여 계산된다.
• \(Y^l\): 이는 \(Z^l\)에 feed-forward 네트워크를 적용한 후 결과에 \(Z^l\)을 추가한 후 다른 레이어 정규화를 적용한 후의 출력을 나타낸다.

• \(Y^l \in \mathbb{R}^{N \times d_{model}}\): \(d_{model}\) 채널을 갖는 \(l\)번째 레이어의 출력이다.
• \(X^0 = \text{Embedding}(X')\): 트랜스포머에 대한 초기 입력이며, 여기서 \(X'\)는 트랜스포머에 의한 처리에 적합한 포맷에 포함된 원시 시계열 데이터이다.
• \(Z^l\): 이상 주의 메커니즘과 피드포워드 네트워크에 의한 처리 후 \(l\)번째 계층에서의 숨겨진 표현.
• Anomaly-Attention: 데이터에서 도출된 실제 연관성과 예상(이전) 연관성을 비교하여 이상 징후를 식별하는 데 중요한 연관성 불일치를 계산하기 위해 고안된 함수이다.
• Anomaly Transformer의 용도: Anomaly Transformer는 시계열 데이터에서 서로 다른 수준의 연관성을 효과적으로 학습하고 비교함으로써 이상 징후 탐지 능력을 향상시키는 것을 목표로 한다. 이는 일반적으로 데이터에서 우세한 정상 동작에 의해 미묘하고 가려지는 이상 징후를 탐지하는 데 특히 중요하다.

Anomaly Transformer

Anomaly-Attention

• Prior-Association: 이는 학습 가능한 가우시안 커널을 사용하여 모델링되었다. 가우시안 커널은 시간적으로 서로 가까운 지점의 중요성을 자연스럽게 강조하는 유니모달 특성 때문에 사용되며, 이는 이상 징후가 시간적 이웃과 밀접한 관련이 있을 것으로 예상되는 패턴을 식별하는 데  유용하다. 학습 가능한 스케일 매개변수 \( \sigma \)를 사용하면 모델이 데이터 포인트의 "이웃"을 얼마나 좁게 또는 광범위하게 고려하는지 조정하여 다양한 이상 세그먼트 길이와 같은 다양한 패턴에 적응할 수 있다.
• Series-Association: 이 모델의 한 부분은 원시 시계열 데이터로부터 직접 연관성을 학습한다. 이는 자신이 관측하는 실제 데이터를 기반으로 적응적으로 가장 관련성이 높은 연관성을 포착하는 것을 목표로 한다. 이는 서로 다르고 진화하는 데이터 패턴에 동적으로 적응할 수 있음을 의미하며, 이는 데이터의 성격이 시간에 따라 변화할 수 있는 시계열에서 매우 중요하다.

• 초기화:
  • Q, K, V: 이 기호들은 주의 메커니즘에서 사용되는 쿼리, 키 및 값 행렬을 나타내며, 시퀀스의 각 요소가 다른 모든 요소와 어떻게 관련되는지 결정하는 데 중요하다.
  • \( \sigma \): 이전 연관성 계산에 사용되는 학습 가능한 척도 매개변수를 나타낸다. 가우시안 함수의 "폭"을 조정하여 시간적 근접성이 연관 가중치에 얼마나 강하게 영향을 미치는지에 관여한다.
• Prior-Association(\( P' \)):
  • 이는 가우시안 커널을 사용하여 계산된다. 공식  \(\frac{1}{\sqrt{2\pi \sigma_i}} \exp \left(-\frac{(j - i)^2}{2\sigma_i^2}\right)\)는 점 \(i \)을 중심으로 하는 정규 분포를 설명하며, \(j \)는 시리즈의 또 다른 점이다. 가우시안 함수는 \(j \)가 \(i \)에서 멀어질수록 감소하여 \(i \)에서 멀리 떨어진 점이 영향력이 적음을 나타낸다.
  • Resale(): 이 가중치들을 각 행에 걸쳐 정규화하여 각 요소의 연관 가중치가 1이 되도록 하여 확률 분포로 변환한다.
• Series-Association(\( S' \)):
  • \( \text{Softmax}\left(\frac{QK^T}{\sqrt{d_{model}}}\right) \)  로 계산된다. 모델 차원의 역제곱근(\(d_{model} \))으로 스케일링된 쿼리와 키의 내적에 적용되는 소프트맥스 함수의 이 부분은 쿼리-키 유사성에 의해 결정되는 것처럼 관련성이 높은 요소에 대한 주의 집중을 용이하게 한다.
• Reconstruction 
  • 연관성이 설정되면, 직렬 연관성 \( S' \)을 사용하여 값 \( V \)을 가중하고, 본질적으로 학습된 연관성에 따라 입력 데이터를 요약한다. 결과 행렬 \( \tilde{Z}^l \)은 주의 메커니즘의 출력에 의해 영향을 받는 입력 데이터의 재구성된 표현을 제공한다.

Minimax association learning

• Multi-Head Attention 세부 정보
  • Q, K, V 행렬: Multi-Head Attention 설정에서 각 헤드에 대한 쿼리, 키 및 값 행렬이다. \(Q_m, K_m, V_m\)는 \(m\)번째 헤드에 고유한다.
  • \(\tilde{Z}_m\): 연결 및 추가 처리 전에 \(m\)번째 Head의 출력을 나타낸다.
  • 연결: 각 Head의 출력을 연결하여 최종 출력 행렬 \(\tilde{Z}^l\)을 형성한 다음 레이어 정규화와 같은 후속 변환을 거친다.

Association Discrepancy

 

• Association Discapancy는 두 가지 유형의 연관성, 즉 사전 연관성과 직렬 연관성 간의 대칭된 Kullback-Leibler (KL) 발산으로 정의된다. 이 메트릭은 이 두 분포 간의 정보 이득을 정량화하고 예상 데이터 연관성과 관측 데이터 연관성의 상당한 차이를 식별하여 이상 징후를 탐지하는 데 사용된다.
• 대칭 KL 발산: 공식은 KL 발산을 사용하여 양방향( \(P'\)에서 \(S'\) 및 \(S'\)에서 \(P'\))까지의 두 확률 분포 간의 차이를 측정한 다음 이를 평균하여 대칭 측정값을 얻는다. 이는 각 분포에서 다른 분포로의 발산을 동등하게 취급하여 불일치에 대한 균형 잡힌 시각을 제공한다.

• \(KL(P'_l \| S'_l)\)은 계층 \(l\)의 사전 결합에서 동일 계층의 직렬 결합으로의 KL 발산으로, 직렬 결합이 사전 결합을 근사화하는 데 사용될 때 얼마나 많은 정보가 손실되는지를 나타낸다.
• \(KL(S'_l \| P'_l)\)은 계열연관에서 사전연관으로의 발산으로, 반대 방향의 정보 손실을 나타낸다.
• \(L\)은 전체 레이어 수이며, 모든 레이어에 걸친 불일치를 평균하여 종합적인 척도를 제공한다.
• 점별 연관 불일치: 이 계산은 시계열의 각 시점(\( \mathcal{X} \))에 대해 수행되며, 각 점에 대한 특정 불일치 측정값을 제공한다. 이상 징후는 예상되는 (이전) 패턴에서 더 크게 벗어나므로 정상 점에 비해 더 높은 불일치 값을 가질 것으로 예상된다.

3.2 MINIMAX ASSOCIATION LEARNING

 

• Reconstruction Loss
  
  • 모델은 Reconstruction Loss를 사용하여 시리즈-연관 학습 프로세스를 안내한다. 이 손실은 재구성된 시리즈 \(\hat{X}\)가 원래 입력 시리즈 \(X\)와 밀접하게 일치하도록 보장하여 데이터에서 정규 패턴을 캡처하고 복제하는 모델의 능력을 향상시킨다.
  • 이는 요소들의 절대 제곱의 합의 제곱근을 측정하는 프로베니우스 노름(\(\|\cdot\|_F\)을 사용하여 정량화되며, 기본적으로 재구성된 급수와 원래의 급수 사이의 차이의 크기를 평가한다.
• Association Discrepancy Loss
  • 모형은 정상 시점과 비정상 시점을 더 구분하기 위해 연관성 불일치 손실을 포함한다. 이 손실 함수는 모형이 전형적인 패턴에서 벗어나는 지점에 대해 이전 연관성과 시리즈 연관성 사이의 불일치를 증가시켜 이상 징후를 더 잘 탐지할 수 있도록 유도한다.
  • 불일치 손실은 요인 \(\lambda\)에 의해 스케일링되며, 여기서 \(\lambda > 0\). \(\lambda\)가 양수일 때, 최적화는 예상되는 (이전) 연관성과 관찰된 (계열) 연관성 간의 차이를 강조하면서 연관성 불일치를 확대하는 데 중점을 둔다.

• 여기서 첫 번째 항은 재구성에서 원본 데이터로부터의 편차를 페널티하여 입력에 대한 충실도를 보장한다.
• 두 번째 항은 \(\lambda\)로 스케일링되어 낮은 불일치 점수를 페널티하여 모델이 이상 징후를 나타낼 가능성이 있는 차이를 강조하도록 한다.

Minimax Strategy

 

• 목표: Minimax Strategy는  이상 징후 탐지에 중요한 사전연관과 계열연관 사이의 연관성 불일치를 최적화하는 것을 목표로 한다. 목표는 사전연관이 한 단계에서 계열연관을 근사화한 다음 다른 단계에서 차이를 최대화하는 것이다.
• 가우시안 커널 조정: 연관성 불일치를 직접 최대화하면 사전 연관성이 무의미해질 수 있으며(즉, 너무 넓거나 너무 좁게), 이는 바람직하지 않다. 따라서, 가우시안 커널의 스케일 파라미터를 조정하는 것은 사전 연관성이 의미 있게 유지되고 시간 패턴을 학습하는 데 효과적으로 기여하는 것을 보장한다.
• 2단계 최적화

• Minimize Phase:
  • 목표: 원시 계열 데이터에서 파생된 계열 연관성 \( P' \)을 근사화한다.
  • 접근법: 연관성 불일치를 최소화함으로써 모델은 이전 연관성을 시리즈 연관성과 더 밀접하게 일치하도록 조정하여 실제 데이터 패턴으로부터 학습한다.
  • 손실함수: \(L_{\text{Total}}(\hat{X}, P, S_{detach}, -\lambda; X) \)
  • 여기서, \( S_{detach} \)는 직렬-연관 부분으로부터의 그래디언트가 정지된 상태(*detach*로 표시)를 나타내어, 이 단계 동안의 업데이트를 방지한다.
• Maximize Phase:
  • 목표: 연관성 불일치를 개선하여 이상 징후를 더 잘 탐지할 수 있도록 한다.
  • 접근법: 이 단계에서 모델은 이전 연관과 시리즈 연관의 차이를 증가시키는 데 초점을 맞추어 시리즈 연관이 비정상을 나타낼 수 있는 인접하지 않거나 덜 명백한 시간 패턴에 더 많은 주의를 기울여야 한다.
  • 손실함수: \(L_{\text{Total}}(\hat{X}, P_{detach}, S, \lambda; X) \)
  • \( P_{detach} \)는 이 단계에서 이전 연관성에 대한 그래디언트 업데이트가 중지되어 직렬 연관성에 학습이 집중됨을 나타낸다.

Association-based Anomaly Criterion

• Association Discrepancy:
  • 정규화된 Association Discrepancy AsDis(P, S; X')는 이전 연관성과 직렬 연관성 사이의 차이를 측정한다. 이 불일치는 관측된 연관성이 예상 연관성에서 얼마나 벗어나는지를 정량화한다.
• Reconstruction Criterion 결합:
  • Association Discrepancy는 시간적 표현과 연관 불일치의 구별 가능한 특징 모두를 이용하여 재구성 기준에 통합된다. 이 통합 접근법은 재구성의 오류와 불일치의 구별 가능성 모두를 활용하여 이상 징후 탐지를 향상시키는 데 도움이 된다.
• Anomaly Score Calculation:
  • 시리즈의 각 데이터 포인트에 대한 최종 이상 점수는 다음 공식을 사용하여 계산된다.

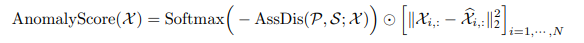
• Softmax Function: 시리즈에 대한 확률 분포로 값을 변환하는 데 적용되어 여러 시점에 걸쳐 점수를 비교할 수 있다.
• 요소별 곱셈(\(\odot\)): 이 연산은 높은 불일치와 유의한 재구성 오류가 모두 일치하는 점을 강조하여 각 데이터 포인트에 대한 재구성 오류 제곱에 연관 불일치를 결합한다.

 

EXPERIMENTS

 

• 5개의 데이터셋을 사용하였다.
• SMD(서버 시스템 데이터 세트):
  • 출처 : Su et al(2019년)
  • description: 이 데이터 세트는 대형 인터넷 회사에서 5주 동안 수집한 것이다.
  • 기능: CPU 사용량, 메모리 사용량, 디스크 활동, 네트워크 활동 등 다양한 서버 메트릭을 포함하는 38개의 차원으로 구성되어 있다.
• PSM(풀링된 서버 메트릭):
  • 출처 : Abdulaal et al. (2021), eBay에서
  • description: 이 데이터 세트는 eBay의 여러 애플리케이션 서버 노드에서 파생되었다.
  • 기능: 여기에는 26개의 차원이 포함되어 있으며, 서로 다른 서버에 통합된 메트릭을 중심으로 성능을 분석하고 운영상의 이상을 감지하는 데 사용할 수 있다.
• MSL(화성 과학 연구소 로버) 및 SMAP(토양 수분 능동 수동 위성):
  • 출처 : Hundman et al. (2018), NASA
  • description: 두 데이터 세트 모두 공개되며 NASA의 Incident Surprise Anomaly(ISA) 보고서에서 파생된 우주선 모니터링과 관련된 원격 측정 이상 데이터를 포함한다.
  • 기능: MSL은 55개의 차원을 가지고 있는 반면, SMAP는 25개의 차원을 가지고 있어 온도, 에너지 판독, 위치 측정 및 기타 중요한 작동 파라미터와 같은 광범위한 원격 측정 데이터를 나타낸다.
• SWAT(안전한 수처리):
  • 출처 : Mathur & Tippenhaur (2016)
  • description: 이 데이터 세트는 수처리 시설에서 가져온 것으로 지속적인 운영 중인 중요 인프라 시스템의 51개 센서에서 얻은 것이다.
  • 특징 : 안전한 수처리 공정을 보장하기 위해 필수적인 유량, pH, 염소 수준, 저장소 수준 및 기타 작동 지표와 같은 다양한 센서의 데이터를 포함할 가능성이 높다.
• NeurIPS-TS(NeurIPS 2021 시계열 벤치마크):
  • 출처: Lai et al. (2021년)
  • description : NeurIPS 2021 컨퍼런스에서 제안된 벤치마크 데이터 세트로, 시계열 이상 탐지를 위해 특별히 설계되었다.
  • 기능: 행동 중심 분류법에 따라 포인트-글로벌, 패턴-맥락, 패턴-셰이플릿, 패턴-시즌, 패턴-트렌드의 5가지 시계열 이상 시나리오가 포함되어 있다. 각 카테고리는 서로 다른 유형의 이상 시나리오를 나타내므로 다양한 이상 탐지 방법을 테스트하는 데 유용한 데이터 세트이다.

Implementation details

 

• 슬라이딩 윈도우를 사용하였다. 이때 크기는 100이다.
• 임계값 \( \delta \)은 시점들을 이상 징후로 레이블링하는 데 사용된다. 이 임계값은 검증 데이터 세트에서 시점들의 특정 비율 \(r \)이 이상 징후로 레이블링되도록 설정된다:
  • SWaT의 경우, \(r \)는 0.1%로 설정된다.
  • SMD의 경우, \(r \)는 0.5%로 설정된다.
  • 다른 데이터 세트의 경우, \(r \)은 1%로 설정된다.
• 이상 징후로 분류된 검증 데이터 세트의 시점. 주요 결과의 경우 r = 0.1%로 설정했다.
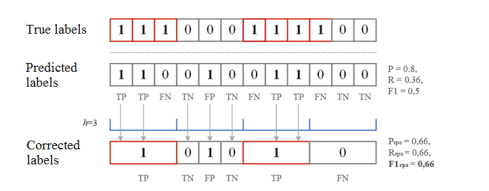
• 이 모델은 데이터의 연속 세그먼트에서 임의의 시점이 이상 징후로 감지되면 해당 세그먼트의 모든 시점이 올바르게 감지된 것으로 간주되는 조정 전략을 채택한다.

• 모델은 3개의 레이어로 구성되어있다.
• Hidden States (\( d_{model} \): 모델의 숨겨진 상태에 있는 유닛의 수는 512개로 설정되어 있다.
• 헤드 수(\(h \): 모델은 다중 헤드 어텐션 메커니즘에 8개의 헤드를 사용하여 데이터의 병렬 처리를 용이하게 한다.
• Hyperparameter \( \lambda \): 손실 함수의 구성 요소의 균형을 맞추기 위해 모든 데이터 세트에 대해 3으로 설정한다.
• 최적화는 ADAM을 사용한다.
• \(10^{-4} \)의 초기 학습률을 사용한다.
• early stopping: 10회 이내에 개선이 관찰되지 않으면 조기에 훈련을 중단하여 과적합을 방지하는 데 도움이 된다.
• 배치크기 : 배치크기는 32로 설정되어 있다.